周昱彤

（云南天朗再生资源有限责任公司）

摘  要  利用拟大地水准面获取GPS测量正常高程是一种不同于传统高程测量的新方法。GPS高程拟合方法的精度能否满足要求，直接关系到GPS高程测量在实际测量中的应用。本文通过工程实例，研究了平面拟合方法、曲面拟合方法和最小二乘法配置拟合方法的区别。通过精度分析，得出上述方法的优缺点，为在实际测量工作中选择合适的拟合方法提供依据。  

关键词  GPS  高程异常  GPS高程拟合方法

1  引言

GPS作为一种新的测量技术和方法，广泛应用于测绘的各个方面。它有能全天候观测，不受视觉条件的限制，测量速度快，效率高的优点。中国采用的坐标系为西安80坐标系，高程系统为正常高程系统，GPS系统为WGS84坐标系，WGS84坐标系为地球高程系统。因此，在中国使用GPS进行测量时，测量结果需要在高程系统之间进行转换，即地球高度与正常高度的转换。如我们所知，大地高和正常高之间存在一个差距，我们称之为高程异常，用ζ表示(图1)。从本质上讲，高程异常主要与地球的结构有关，即地球的密度和重力。要拟合大范围的高程异常，必须考虑重力因素，然而，在小范围内或当重力异常变化很小时，数学模型可以直接用于模拟表面以求解高程异常，而不考虑重力的影响。本文主要采用三种方法进行曲面拟合，一种是最小二乘法平面拟合方法；一种是最小二乘法曲面拟合方法。还有一种最小二乘法配置拟合方法。通过对三种方法的比较，得到了一种不考虑重力因素的精确的局部GPS高程拟合方法。

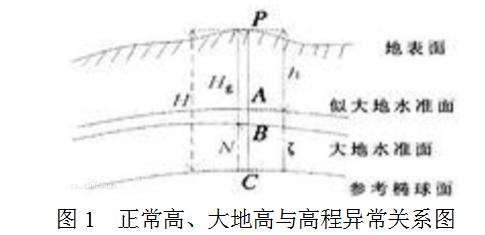
 图中，H表示大地高，Hξ表示正高，h表示正常高，ξ表示高程异常，N表示大地水准面差距。

2  GPS高程拟合的原理及方法

2.1平面拟合法

平面拟合法是最早期进行高程拟合采用的的方法，其基本原理是利用最小二乘法。平面拟合法的数学模型为：

已知高程异常的水平重合点为n(n≥3)，利用最小二乘法求拟合系数，即可得到未知高程异常。

2.2二次曲面拟合法

二次曲面拟合法的数学模型为：

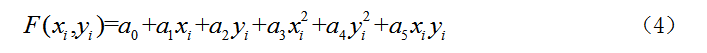
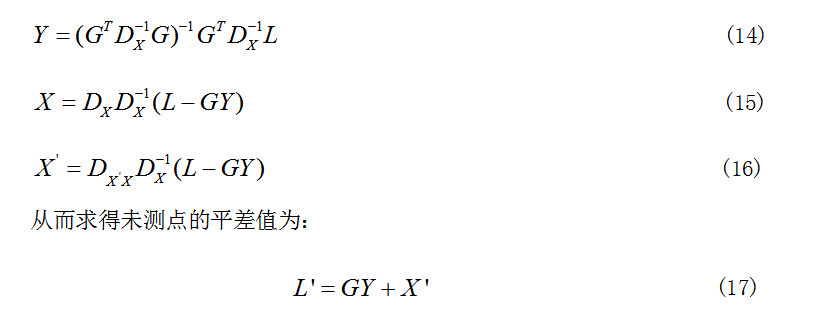
3  工程实例

3.1工程概况

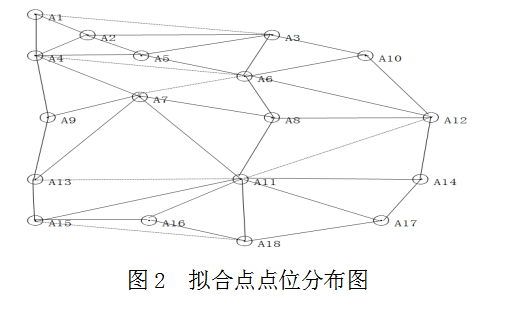
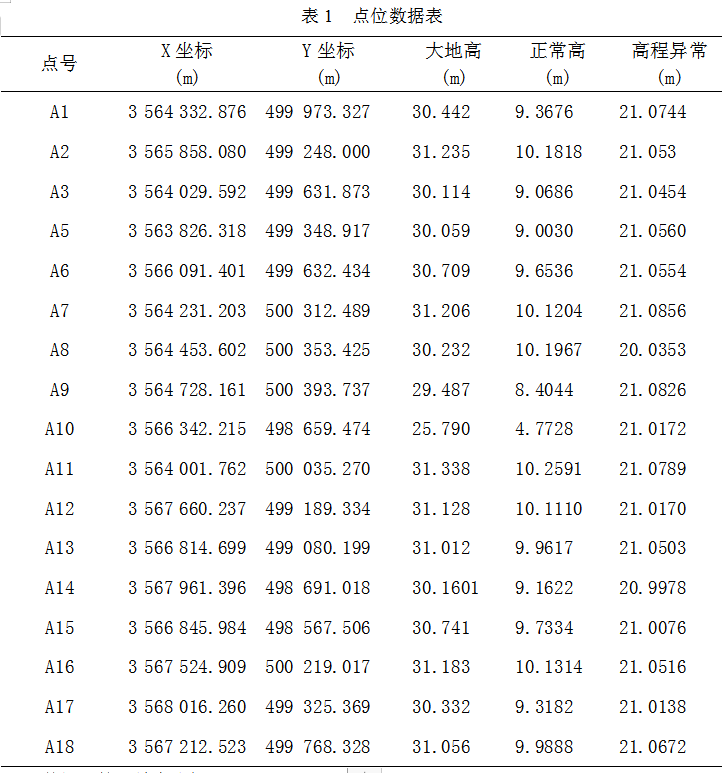
在地形相对平坦的测区，GPS控制网中有18个精度相同、无粗差的水准点，平均边长约0.6KM。本次测量按照国家GPS网C级要求进行，所有GPS点均采用四等水准联合测量，即18个点的分布图见图2，其坐标和大地高、正常高(水准测量)和高程异常见表1。

3.2数据计算及精度分析                     

为了消除点位分布因素的影响，选取均匀分布在整个测试区域的7个已知点作为拟合点，另外选取11个点作为样本点进行检验。由于GPS高程与水准重合点较少，直接采用平方根函数作为协方差函数模型，即:

其中，v 为拟合残差，n 为参与拟合点的个数，m 为拟合外推点的个数。内、外符合精度越小，表明拟合和预测的精度越高；反之，则说明拟合和预测的精度越差。

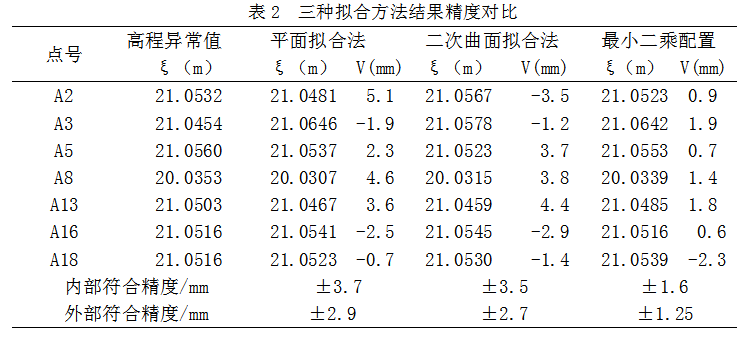
由表2可以看出:(1)采用上述三种方法进行拟合，拟合精度可以满足四级几何水准测量的要求;(2)从上述三种方法的拟合结果可以看出，最小二乘法拟合精度最高。平面拟合方法的拟合精度与二次曲面拟合方法相近。在某些情况下，平面拟合精度高于二次曲面拟合方法。可以得出，在不考虑重力影响的情况下，对于地势较为平缓的区域，平面拟合方法的精度可能要高于二次拟合方法，但最小二乘法配置规则不受地形因素的影响。

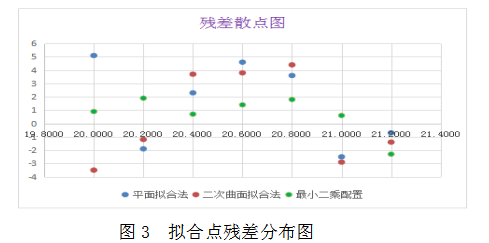
由图3可以得出：在以上三种拟合方法中，平面拟合法和二次曲面拟合法残差值分散，变化较大，不稳定；最小二乘法配置残差值变化较小，残差值在一定范围内波动，比较平稳。

4  结论

本文以实测区域数据为例，对三种GPS高程拟合方法进行了对比分析。同一区域的高程异常既有趋势性(即与坐标函数相关的非随机性)，也有随机性。考虑到高程异常的趋势性和随机性，理论上更合理，实践上更可靠。拟合结果表明:

(1)在平面拟合模型中，只考虑高程异常趋势。模型采用平面来表示大地水准面，因此在地形相对平缓的局部区域精度较高，而在高程起伏较大、面积较大的区域精度较低。

(2)二次曲面拟合是利用二次曲面函数模型来拟合似大地水准面的曲面。理论上，二次曲面更接近真实的似大地水准面，因此，该方法的精度相应更高。然而，该模型只是一个逼近模型，在某些点上，尤其是在相对平缓的局部区域，其拟合精度可能不如平面拟合模型高。

(3)最小二乘法配置是一种函数模型逼近大地水准面的随机综合模型。即该模型既考虑了高程异常的随机性，又考虑了高程异常的趋势，适用于不同的地形。因此，在上述三种方法中，最小二乘法配置拟合精度最高，适用范围较广。

5  参考文献

[1] 史俊莉，李生平．考虑地形改正的ＧＰＳ高程拟合研究 ［Ｊ］．测绘通报，2015(7)：66-67

[2]张红华,孙月文.GPS高程拟合方法及精度分析[J].测绘与空间地理信息,2014,37(2):132-135.

[3] 何美琳,文鸿雁,潘元进,等.GPS高程拟合的方法比较[J]. 测绘科学,2013,38(3):63-65

[4] 杨江波，李为乐，余代俊，等.GPS 高程拟合方法的实验研究[J].测 绘科学，2009，34（3）：54-57.

[5] 沙月进·最小二乘配置法在GPS高程拟合中的应用[J].测绘信息与工程, 2000, (3): 3-5·

[6]孙正明.最小二乘配置法在GPS高程异常推估中的应用[J].测绘科学,2007,32(6).

[7]隋立芬,宋力杰.误差理论与测量平差基础[M].北京:解放军出版社,2004.